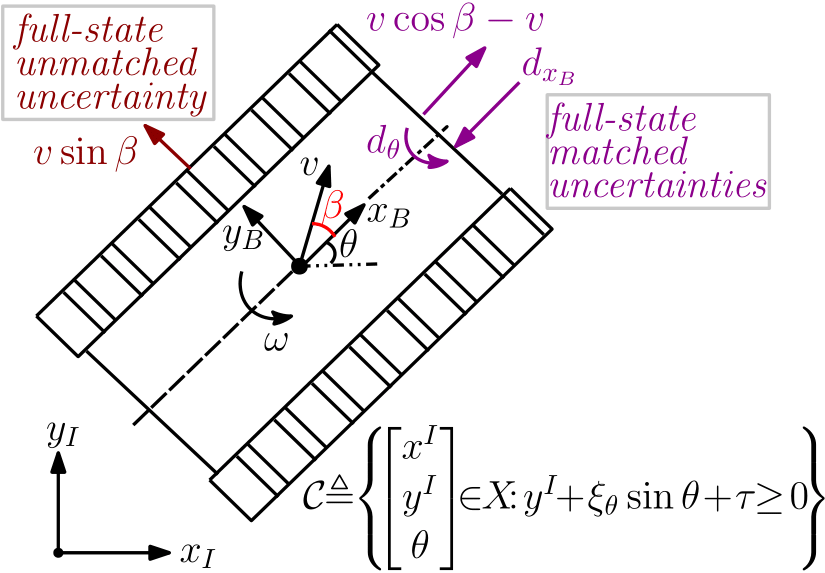
This paper proposes a safety-critical control design approach for nonlinear control affine systems in the presence of matched and unmatched uncertainties. Our constructive framework couples control barrier function (CBF) theory with a new uncertainty estimator to ensure robust safety. The estimated uncertainty with a derived upper bound on the estimation error is used for synthesizing CBFs and safety-critical controllers via a quadratic program-based feedback control law that rigorously ensures robust safety while improving disturbance rejection performance. The method is extended to higher-order CBFs (HOCBFs) to achieve safety under unmatched uncertainty, which may cause relative degree differences with respect to control input and disturbances. We assume the relative degree difference is at most one, resulting in a second-order cone constraint. The proposed robust HOCBF method is demonstrated via a simulation of an uncertain elastic actuator control problem. Finally, we experimentally demonstrated the efficacy of our robust CBF framework on a tracked robot with slope-induced matched and unmatched perturbations.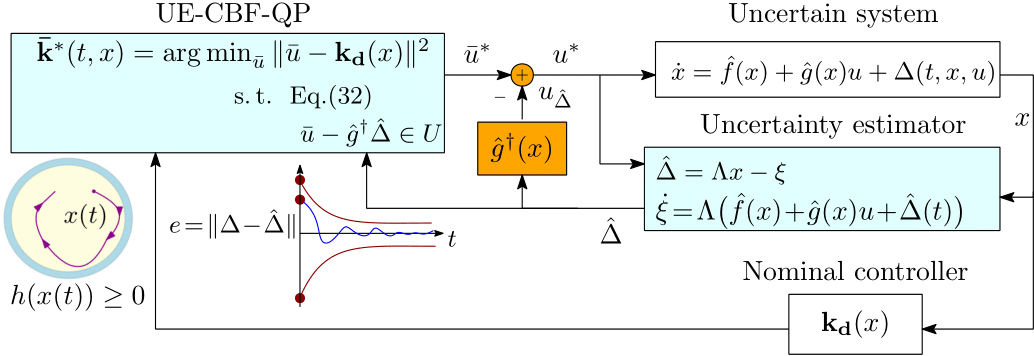

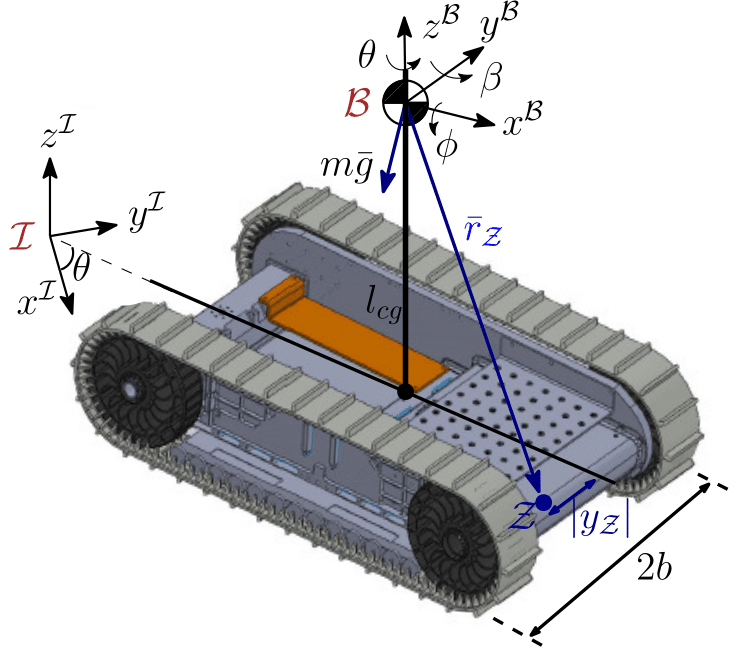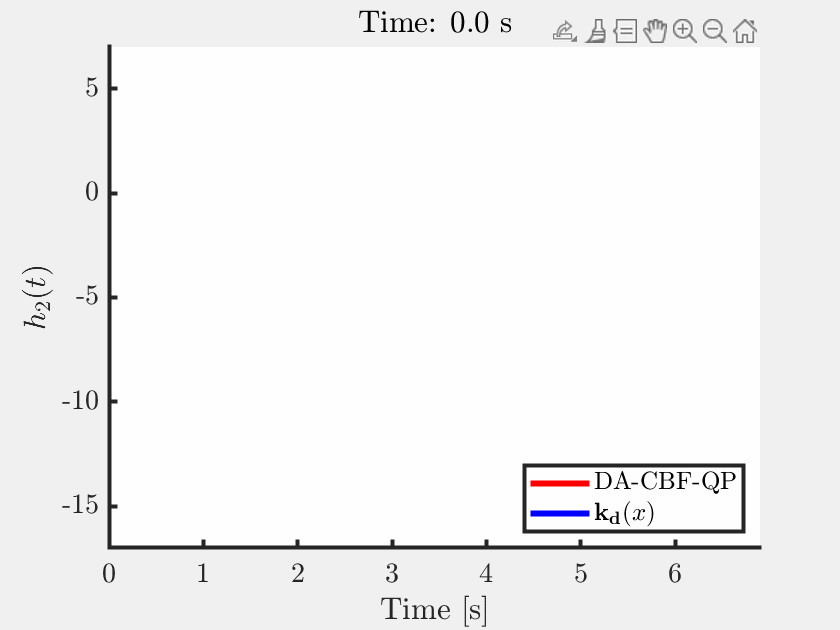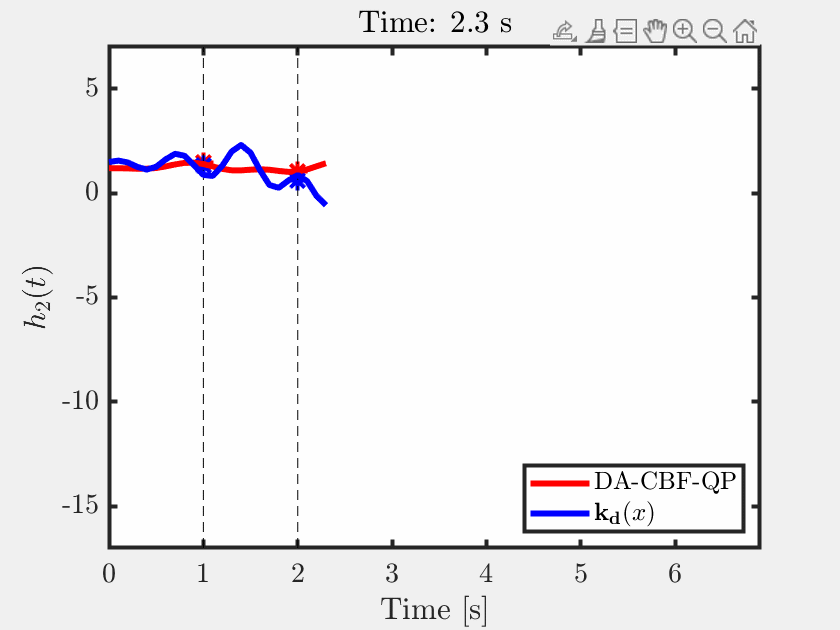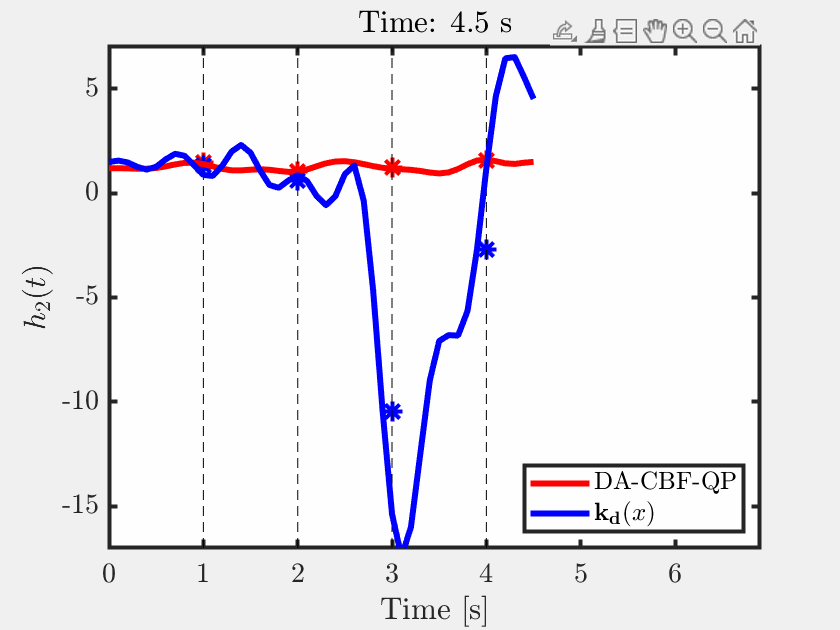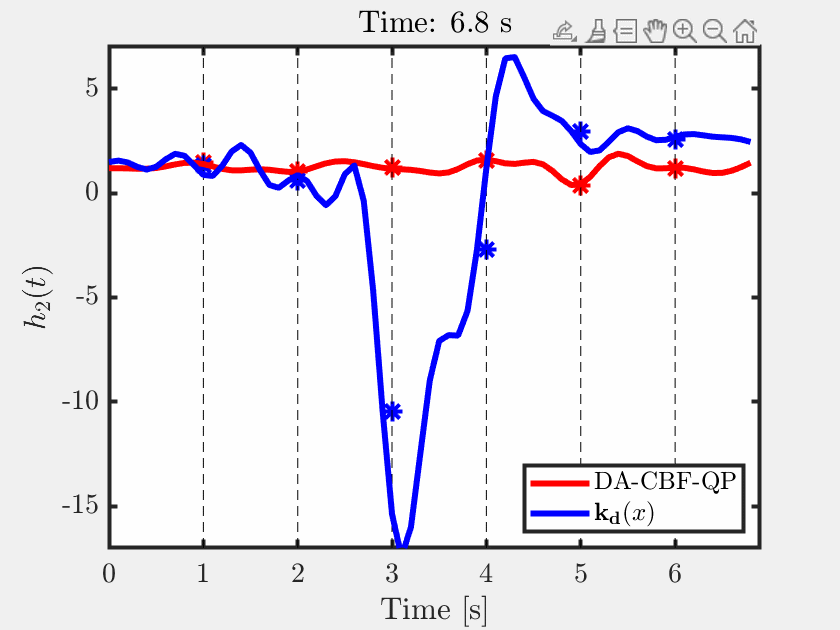This paper develops rollover prevention guarantees for mobile robots using control barrier function (CBF) theory, and demonstrates the method experimentally. We consider a safety measure based on a zero moment point condition through the lens of CBFs. However, these conditions depend on time-varying and noisy parameters. To address this issue, we present a differentiator-based safety-critical controller that estimates these parameters and pairs Input-to-State Stable (ISS) differentiator dynamics with CBFs to achieve rigorous safety guarantees. Additionally, to ensure safety in the presence of disturbances, we utilize a time-varying extension of Projection-to-State Safety (PSSf). The effectiveness of the proposed method is demonstrated via experiments on a tracked robot with a rollover potential on steep slopes.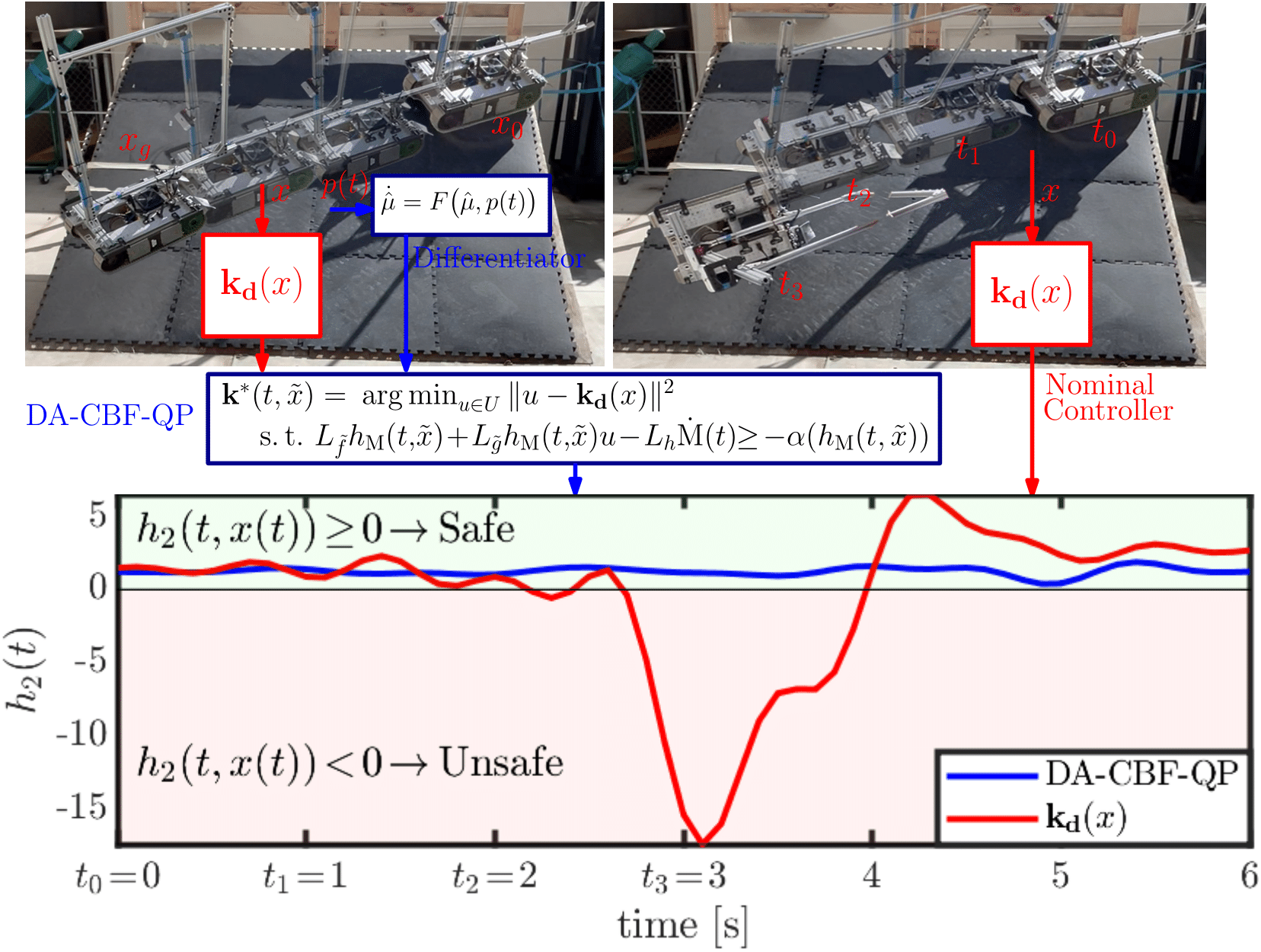

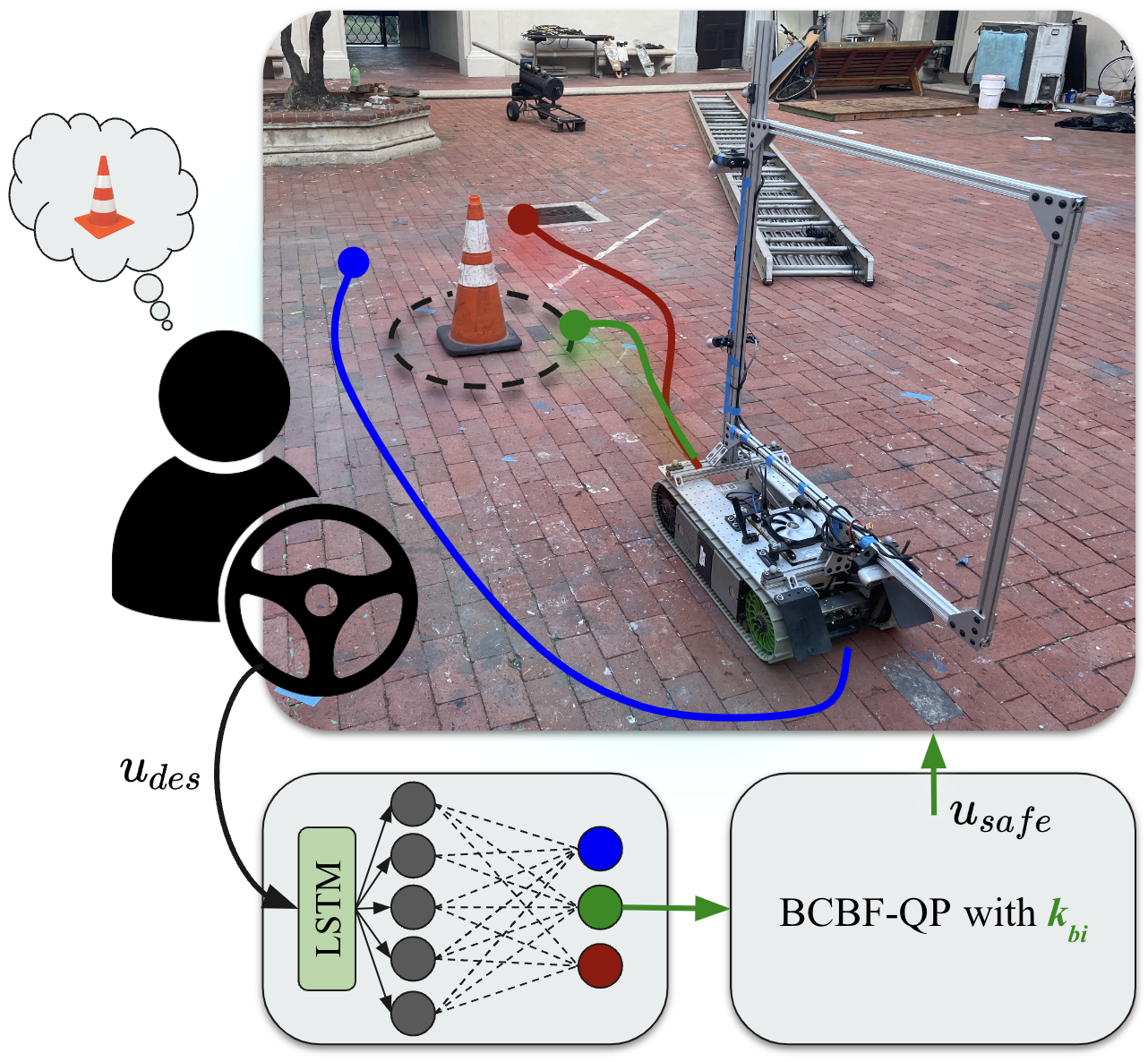Ensuring robot safety in complex environments is a difficult task due to actuation limits, such as torque bounds. This paper presents a safety-critical control framework that leverages learning-based switching between multiple backup controllers to formally guarantee safety under bounded control inputs while satisfying driver intention. By leveraging {\em backup controllers} designed to uphold safety and input constraints, \textit{backup control barrier functions} (BCBFs) construct implicitly defined control invariant sets via a feasible quadratic program (QP). However, BCBF performance largely depends on the design and conservativeness of the chosen backup controller, especially in our setting of human-driven vehicles in complex, e.g, off-road, conditions. While conservativeness can be reduced by using multiple backup controllers, determining when to switch is an open problem. Consequently, we develop a broadcast scheme that estimates driver intention and integrates BCBFs with multiple backup strategies for human-robot interaction. An LSTM classifier uses data inputs from the robot, human, and safety algorithms to continually choose a backup controller in real-time. We demonstrate our method's efficacy on a dual-track robot in obstacle avoidance scenarios. Our framework guarantees robot safety while adhering to driver intention.

This paper develops a Bayesian optimal experimental design for robot kinematic calibration on $\mathbb{S}^3 \!\times\! \mathbb{R}^3$. Our method builds upon a Gaussian process approach that incorporates a geometry-aware kernel based on Riemannian Mat\'ern kernels over $\mathbb{S}^3$. To learn the forward kinematics errors via Bayesian optimization with a Gaussian process, we define a geodesic distance-based objective function. Pointwise values of this function are sampled via noisy measurements taken through fiducial markers on the end-effector using a camera and computed pose with the nominal kinematics. The corrected Denavit-Hartenberg parameters are obtained using an efficient quadratic program that operates on the collected data sets. The effectiveness of the proposed method is demonstrated via simulations and calibration experiments on NASA's ocean world lander autonomy testbed (OWLAT).

Improvement of precise reference tracking performance of positioning systems is one of the essential objectives in feedback control design process. However, since the robustness of the feedback control system normally limits the fine positioning capacity, improvement in reference tracking performance with the desired robustness is difficult to be achieved. This paper proposes a new data-driven approach based on convex optimization to design two degree of freedom robust fixed-order $\mathcal{H}_\infty$ controller for reference tracking. Linear time-invariant systems represented by non-parametric frequency domain data are considered. A semi-definite programming algorithm is employed to compute an optimal uncertainty model and the corresponding nominal model. Then, a novel sufficient robust performance condition is developed using Nyquist stability theorem and $\mu$-synthesis methods for feedforward control systems. The proposed method allows formulating closed-loop model matching objective and robust performance conditions by convex functions. In addition, the presented two degree of freedom robust data-driven fixed-order controller design algorithm also can be directly applied to time-delay systems without any approximation and conservatism. The theoretical design approach is experimentally verified on position control of an electromechanical control actuation system of an air vehicle. To improve the positioning accuracy of the actuation system, the full-closed loop feedback structure is considered. Obtained experimental results verify the usefulness and efficiency of the proposed approach.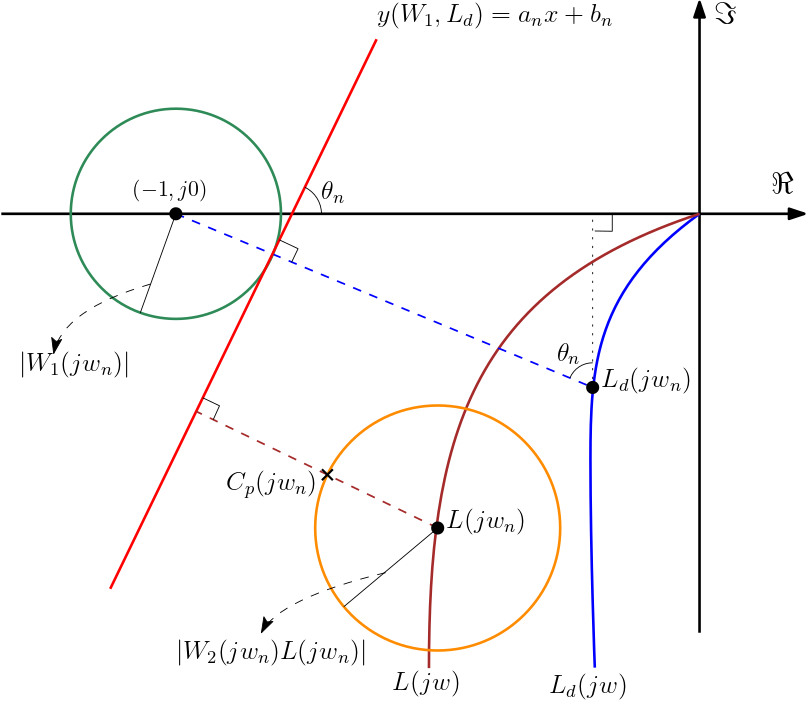